I. Introduction

II. The Usual Economics Framework

all of the studies I know of the value of perfect information find its value to be on the order of one percent of the value of output. For example, ... one study found that if you halve the standard error of precipitation and temperature, say from one percent to half percent, or one degree to one-half a degree, you get an improvement in the value of the output on the order of 2 percent of the value of wheat production. A study of cotton gave the same order of magnitude. I have looked at a number of studies in the area of nuclear power and energy, trying to determine the value of knowing whether nuclear power is ever going to pan out. Again, perfect information is worth on the order of one percent of the value of the output. From these kinds of studies, then, we find the value of information is not zero, but it is not enormous either.

To be sure, a small percent of a large number is a large number -- so the value of forecasts to these industries may indeed represent a lot of money. In the case of wheat production, for instance, 2% of the U.S. farm value of output in 1994 ($8.2 billion) is $164 million; the same percent of all U.S. farm income (grains, vegetables, fruits, and livestock), which totaled $175 billion in 1994, would be $3.5 billion. But estimated total annual revenue for specialized U.S. meteorological services, to which most large scale farms are likely to subscribe, is only on the order of $400 million.

By similar reasoning, Roll (1984, p. 879), in a study of the behavior of futures markets for orange juice and the effect of weather information on these markets, concludes that "… there is a puzzle in the orange juice futures market. Even though weather is the most obvious and significant influence on the orange crop, weather surprises explain only a small fraction of the observed variability in futures prices." If Nordhaus's point is borne out, then compared to the value of final products, whether measured as the value of production or capitalized into futures prices, the incremental gain from information appears to be quite small.

This observation sharply contrasts with another view, illustrated in an editorial by the administrator of the National Oceanic and Atmospheric Administration, D. James Baker. Writing shortly after heavy rains had flooded many parts of California in the winter, 1995, he commented "If we'd been able to produce a forecast last spring that California would be deluged this winter, it would have been worth whatever research investment was involved, if only because of the human misery it would have relieved" (Baker, 1995). Such a conclusion might be easier after the fact ("If only I had known" about the weather, a stock market pick, a lottery number)². It is much more difficult to arrive at such a conclusion before the fact, however. In general, it is only ex ante -- before the event -- that we are willing to pay for information, because afterwards it doesn't matter.

Indeed, the ex ante, or expected value, is what experts agree determines the value of information. If the probability of an event is either very unlikely or very likely, or if the actions that can be taken to avert its effects are minimal, then this value can be quite low. The value of a flood forecast is small if flooding is either highly unlikely or very likely in a geographic region, or if the effects of flooding are almost impossible to prepare for (for instance, in the case of Bangladesh due to factors such as the quality of the housing stock, other infrastructure, and population density).

IIa. The Canonical Model

The value of information, then, is essentially an outcome of choice in uncertain situations. Individuals may be willing to pay for information depending on how uncertain they are, and on what is at stake. They may be willing to pay for additional information as long as the expected gain exceeds the cost of the information -- inclusive of the distilling and processing of data to render it intelligible information. Moreover, an individual usually has subjective probabilities about the quality of the information, and will make use of additional information by using it to "update" his prior beliefs.

The mathematical formulation that underlies this framework is a state-preference approach. In such models individuals are assumed to form subjective opinions about the probabilities of two states of the world -- say, "rain" and "no rain." The value of information is in permitting the person to revise estimates of these probabilities.

Formally, the typical model is something like this:

where y is income, A is the state of the world (say, A₁ is crop yield if it rains; A₂ is yield if it doesn't rain), p is the probability of rain; and in the budget constraint, P's are prices of information (I) and all other goods and services (X).

The result after deriving first order conditions is that the person should buy additional information until the expected marginal gain from another piece of information is equal to its cost. Usually expected value is represented by a utility function, about which different assumptions can be made as to its functional form, which in turn can proxy the individual's attitude towards risk (he can be a risk lover, or be risk averse, or be risk neutral).

One of the best textbook examples of how this formulation operates is reproduced in table 1 and figure 1 (Quirk, 1976). Suppose a farmer can harvest his entire crop today at a cost of $10,000 or half today, half tomorrow at a cost of $2,500 per day. The harvested crop is worth $50,000. Table 1 indicates the "payoff" to the farmer in the event of heavy rain. In expected value terms, these payoffs are $40,000 to decision A and p ($22,500) + (1-p) ($45,000) to decision B. If p = 5/22.5, then the decisions give the same payoff³.

If it is possible to forecast the weather, then p is the probability that the information the farmer receives is that there will be a heavy rain tomorrow with certainty (and 1-p is no rain, with certainty). Since it is a subjective probability, p can vary among different farmers. The expected payoff with information is then:

p ($40,000) + (1-p) ($45,000)

If $x is the most the farmer would pay for information, then $x is equal to the difference between the expected payoff with information, and the expected payoff without information. The value of information varies with p as in figure 1.

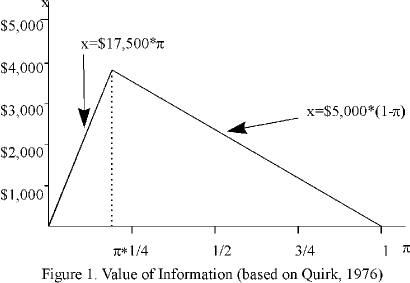
The value is maximized at p = 5/22.5 (where $x = $3,888); as from above, this is the p at which the farmer flips a coin. Information can thus make the biggest difference here. The value of information is zero at p = 0 and p = 1, since at these extremes, the farmer is already certain in his own mind whether it is going to rain, and information is extraneous (even if the farmer is wrong).

Applications of the model can show the effects of changing the amount or quality of information as well as subsequent revisions that the individual may make of the probability (so-called Bayesian updating).

The implications for the value of information from this approach are:

A. Information is without value
--- when individual's subjective beliefs are at extremes (p=0 or p = 1)
--- there are no costs associated with making the wrong decision
--- there are no actions that can be taken in light of the information
B. Information has less value
--- when individual's subjective beliefs are close to extremes
--- when the costs of making the wrong decision are low
--- when actions to take are very limited
C. Information has the most value
--- the more indifferent is the decision maker among his alternatives (flips a coin)
--- the larger are the costs of making the wrong decision
--- the more responsive are the actions that can be taken

IIb. Nonappropriability and the Value of Information

In the context of the model above, the farmer might be willing to pay as much as $2,000 or more for information depending on the value of p. He could then resell the information for, say, $1,999, and other farmers would be willing to buy it from him since it is cheaper than buying it from the original supplier. This can pose a problem in the supply and pricing of information. Since every farmer can argue the same way, it may be impossible to sell the information for any positive price even though it is worth over $2,000 to each farmer. This characteristic of information -- nonappropriability -- results because one person's use of information doesn't diminish the usefulness of the information for someone else to use. A weather forecast, for example, can usually be shared by everybody within a geographic region.

There is a spectrum of nonappropriability of information. For instance, information about a mineral deposit, an oil prospect, or a hot stock, if acted upon by one party, may diminish the usefulness of the information to others. In these types of situations, people may be willing to pay for early and perhaps exclusive access to information, and subsequent buyers may not be willing to pay anything. Buyers may also be willing to pay for information when additional value is added to it (that is, it is specially interpreted and packaged). Some examples are specialized weather data supplied to the trucking, aviation, maritime, and construction industries, or competing macroeconomic forecasts of aggregate economic statistics (the money supply, inflation, interest rates, unemployment). Another exception to the general nonappropriability of information occurs when the supplier can specify and enforce property rights -- for example, issue licenses to use data and to restrict its resale, as is done in the case of software⁴.

Because the supply of much information is subject to the nonappropriability problem, most experts conclude that many types of information are a public good and that government should supply it. Census data are the only data for which government supply is constitutionally mandated, but government has also come to be relied upon for a host of other data, including national weather data; climate, environmental, and space science data; and statistics on health, education, agricultural production, etc.⁵ A recurrent problem in these cases, however, is that it is hard to know if the benefits of the data justify their cost. Most data are made available at the cost of reproduction (as required by Office of Management and Budget Circular A-130). Very little is known about the "true" value of the data. This gap in understanding the value of the data haunts agencies and the Congress in annual budget deliberations.

The nonappropriability of public weather forecasts and other weather- and climate-related data has made it difficult to estimate empirically the value of these types of information. The next section describes some approaches; all of them are based on the general economics of information framework in the preceding discussion.

III. Empirical Approaches to Measuring the Value of Weather Information

IIIa. Revealed Preference

i. Brute force -- directly observed values

Explicit evidence of the value of weather data can be captured in some cases by direct measures of peoples' willingness to pay for it. The net revenues earned by the private weather forecasting industry are an example. From these can be gleaned, say, "annual expenditures by the major trucking companies for specialized weather forecasts." Other examples of willingness to pay to avoid the consequences of unfavorable weather are weather-related insurance premia paid in the event of rain during a sporting event or festival, or monetized values of the extra trouble people go to in carrying an umbrella, winter coat, etc.

Another measure associated with a daily forecast is the per- minute revenue and audience ratings associated with weather on the news, or "expected annual ad revenue per household associated with TV weather broadcasts." For instance, the local evening news broadcasts in the Washington, DC area allot between 2 and 3 1/2 minutes to weather; in New York City, about 1 1/2 minutes is allotted. Producers report that the differences are based on market research, presumably including data collected about how many viewers are gained or lost during weather segments. In New York, viewers want only the "bottom line," which can take less than one minute. In DC, viewers are willing to listen to explanations of the forecast as well as the bottom line. Bob Ryan, the most popular broadcast meteorologist in DC, gets "whatever amount of time he wants" on heavy weather days and averages about 3 1/2 minutes on normal weather days.(Conversations with Dave Jones, WRC-TV meteorologist). These minutes could be capitalized by multiplying by the per minute advertising rate to estimate the value of broadcast weather in different markets.^{6   7}

An important caveat concerning these measures is that they do not capture another dimension of the value of weather information, namely the net social surplus or amount by which society as a whole is better off with the information, after having made the investment to get it. The total social surplus would be estimated by integrating under the demand curves along which the measures suggested above are but single points. From this total measure could be subtracted the total cost of providing weather information to derive net social surplus. The information needed to make these calculations is difficult to obtain, but such net surplus measures would be useful in guiding public investment in weather instruments, spacecraft, and analysis and distribution facilitates.

The measures described above do, however, reveal actual choices made by people who are more or less free to choose the quantity of weather information they prefer. Indirectly observed measures, such as those described next, are also based on actual behavior but are inferred from some model of the relationship between the information and uses to which it is put.

ii. Other measures of capitalization -- indirectly observed prices

Other approaches to valuing weather information use indirectly observed prices. This is the gist of the majority of studies to date; the specific approach is to estimate productivity gains associated with weather forecasts and infer the value of weather information based on the monetized value of these gains. Johnson and Holt (1986) note twenty such studies dating from the 1960s on, including applications to bud damage and loss; haymaking; irrigation frequency; production of peas, grain, soybeans, grapes (raisin), fed beef, wool, and fruit; energy demand; and construction. More recently, Adams and co-authors (1995) observe changes in crop yields associated with phases of the El Nino- Southern Oscillation (ENSO), and use the market value of the yield differences to estimate the commercial value of the ENSO phenomenon.

Other studies use the time-series behavior of commodity prices in futures markets to infer weather-related values. Two examples are Roll (1984), who, as noted earlier, studies orange juice futures, and Bradford and Kelejian (1978), who study stock prices of wheat.

Another large literature dating from the 1970s uses wages and housing prices to infer the value of weather information, under the hypothesis that it is capitalized into the prices of such goods and services. These studies are premised on hedonic price theory, by which researchers model the equilibrium market for a commodity and then derive and estimate a function relating price to characteristics of the commodity. Coefficients on the characteristics are then interpreted as dollar estimates of the implicit value of the characteristics.

Rosen's (1979) study is among the seminal theoretical and empirical research that considers the extent to which interurban wage differences capture urban quality of life. He offers a conceptual framework that takes into account an important fact but one that can be difficult to disentangle empirically, namely, that wages, like prices, are the result of supply and demand. He then develops an econometric model derived from the wage equation often studied by labor economists but expanded to include additional explanatory variables.

Specifically, Rosen regresses an interurban cross-section of average wages on a set of explanatory variables which include not only personal characteristics influencing wages, such as education and age, but also measures of urban amenities and disamenities. These "quality of life" factors include pollution (water pollution, particulates, sulfur dioxide, inversion days); the crime rate; crowding (population density, population size, central city density); market conditions (the unemployment rate and population growth); and climate (number of rainy and sunny days and number of extremely hot days). Higher wages are expected in cities with disamenities compared with nicer cities, and this compensating differential is expected to work in the opposite direction for urban amenities -- a city with pleasant weather, for example, may not have to offer higher than average wages to attract workers and may even be able to offer lower wages. Rosen finds that climate variables are statistically significant in the expected directions; wage rates are higher, for instance, in cities where the weather is rainy or extremely hot.

In one of the most recent studies linking housing prices, Blomquist and co-authors (1988) estimate interurban "quality of life" indices using household's monthly housing expenditures (rent for tenants; imputed rent for homeowners) and measures of climate, environmental quality, crime, and other variables. The climate measures include precipitation, humidity, heating degree days, cooling degree days, wind speed, and sunshine. All of the climate variables are found to be statistically significant determinants of housing expenditure, with an inverse correlation between expenditure and precipitation, humidity, and heating and cooling degree days and a positive correlation between expenditure, wind, and sunshine.

Blomquist and co-authors also include wages in their study, and combine the housing expenditure and wage data in a model that estimates the "full implicit price" of urban area quality of life variables. They find negative prices (that is, a marginal net disamenity) for precipitation, humidity, heating and cooling degree days, and wind speed.

These hedonic approaches to valuing amenities are not without problems of data availability, modeling assumptions, and econometric issues. Freeman (1993) surveys and critiques the methodology of most of the studies to date linking wages and housing prices with environmental amenities. Nonetheless, the approaches could be useful in estimating the value of weather information; for instance, while neither the property value nor wage studies directly shed light on the value of a weather forecast, the approaches could be extended to include weather variability, say, and thus more closely proxy the value of information associated with weather. In addition, the hedonic approaches could be used to ascertain different values associated with different attributes of a forecast -- timeliness, frequency, accuracy⁸.

IIIb. Hypothetical Approaches -- Contingent Valuation

Rather than draw data from observations of real-world choices, hypothetical approaches use people's responses to hypothetical questions. For example, people can be asked how much they are willing to pay for a specific change in environmental quality. The responses, if honest, are expressions of the value that respondents associate with the change. This approach has been called the survey method, the interview method, and other names, but is known most typically as contingent valuation (CV). CV has not yet be used for valuing weather information, although other dimensions of environmental quality have been a popular field for CV research.

CV methods have a long history, beginning in the 1960s with questionnaires used to estimate the benefits of outdoor recreation in Maine.⁹ Other applications of CV have included assessing the value of visibility at the Grand Canyon; national water quality; information about natural hazards (earthquakes); and hunting, fishing, and other recreational permits. Most recently, CV studies were done by parties to the litigation over damages and penalties to land, water, habitat, and other resources as a result of the Exxon Valdez oil spill. The method was also the recent focus of an advisory panel convened by the National Oceanic and Atmospheric Administration to consider the general problem of how best to assess natural resource damages.

CV is fraught with significant controversy. A substantial amount of research and testing of how best to design surveys to elicit honest expressions of valuation has taken place, and where possible, the results of CV studies have been compared with results from direct valuation studies such as those described above. The jury is still out on the acceptability of the approach, although its proponents rightly note that in many cases, there is no alternative means of eliciting values about some types of public goods, including natural resources and other environmental amenities. In addition, design and administration of a high quality CV survey can be quite expensive.

Subject, then, to these advantages and disadvantages of CV studies (and of course, the direct valuation studies have their own limitations), it may be interesting to apply CV to peoples' valuation of weather information. In addition, just as the direct valuation studies use a hedonic approach to understand differences in values associated with different attributes of a good or service, so, too, can CV. In other words, different attributes of a weather forecast -- timeliness, accuracy, frequency -- could be the subject of a CV survey. Its results could be compared with those obtained from the direct valuation studies.

IV. Conclusions

There is less state-of-the-art agreement about how best to estimate empirically the value of information. Obtaining from individuals their actual willingness to pay is problematic, although the news media through viewer ratings may have a brute force approach appropriate for their purposes. Among other approaches, both revealed preference and CV tools have strengths and weaknesses. The revealed preference approach -- which has dominated research to date -- has the advantage of being based on actual decisions. However, the researcher is limited to using data on market situations that may not precisely isolate the value of information from other factors. Examples are other determinants of productivity gains, in studies of the role of weather data in changes in agricultural output; or determinants of property values or wage rates, in studies of the effect of weather on quality of life. The CV approach, yet to be applied to weather information, can be tailored to address the specific question of interest. For instance, it can be administered to a general population sample or to a sub-sample, and it can address changes in the amount and nature of information (e.g., frequency, accuracy). The principal disadvantage is that the CV approach is based on what people say rather than what they do, and CV can be very expensive to design, administer, and evaluate. As the case with applications of CV to other goods, if CV is applied to weather information, the results might be usefully compared with results from revealed preference approaches and the media's ratings scheme.

Finally, the brief overview presented here of approaches to modeling and measuring the value of information has not addressed how individuals "process" information and incorporate it into their expected value calculations. The lack of this so-called transfer function is a gap in most models of information economics. There is a growing literature on adaptive responses by consumers to risk, and new investigations of ways to increase public interest in and understanding of science and weather.¹⁰ These lines of research are generally interdisciplinary, and, taken together, are important extensions of the framework outlined here.

Foot Notes

2 - Although archived data frequently have research value.

3 - This assumes the farmer is "risk neutral." If he is risk averse, he would want a lower value of p before he would wait to harvest. The expected utility model described here is a usual point of departure for studies of individuals' responses to risk in a host of contexts, not just weather forecasts. For example, see Brookshire and coauthors.

4 - Legal protection is not an unequivocal good, however, as it limits the fullest use of information.. Because it would be costless to share the information, imposing costs leads to some losses to society. Legal protection thus requires a trade-off in the supply of and maximum use of data.

5 - The supply of weather data by government was dramatized in the early 1980s when the Communications Satellite Corporation proposed to buy the government's land remote sensing and weather satellites in order to obtain economics of scale and scope in their joint operation. Cartoonists lampooned the proposal with sketches of a citizen scarching franatically for a dollar to buy a vending machine forecast as a mean-looking hurricane bore down on him.

6 - Another measure now discussed in the broadcast industry is the number of accesses to media station's Internet sites. According to NBC/WRC meteorologist Dave Jones (interviewed in Conton, 1996), web hits after the heavy snows in January, 1996 went from 5,000 per day to 50,000 per day at the Washington DC affiliate of NBC (http://wxnet4.nbc4.com). Web hits are highly imperfect measure of the public's value of weather information for several reasons: web hits may be made accidentally or in passing rather than deliberately made on the basis of true interest and information value; a variety of information is poted on the site, not just weather data; and web hits through Internet access are priced at close to zero marginal cost, encouraging people to over-consume. Nonetheless, much of the huge increase during the January 1996 snows is probably indicative of sicere interest in the forecast!

7 - The British Meteorological Office has considered selling weather data to companies which sell commodities such as pet food and tissue paper, having observed correlations between weather and consumer spending patterns. See "Raining Cat and Dog Food," The Economist, 15 March 1997, p. 68.

8 - Ausubel (1986), for example, shows the significant variation associated with the value of weather forecast given its standard deviation; Nelson and Winter (1964) use an expected value approach (described above) to show which attributes of a forecast matter most to the trucking industry.

9 - Mitchell and Carson (1989) reline the history of CV and offer an excellent overview of the literature and approach. Cummings and coauthors (1986) and more recently, Freeman (1993) are also excellent references.

10 - See, for instance, Viscusi and O'Conner (1984), and the NASA/NOAA/NBC project on public use of remote sensing data and the internet (in Conton, 1996, and at http://wxnet4.nbc4.com).

References

Societal Aspects of Weather

Workshop's Main Page

Table of Contents