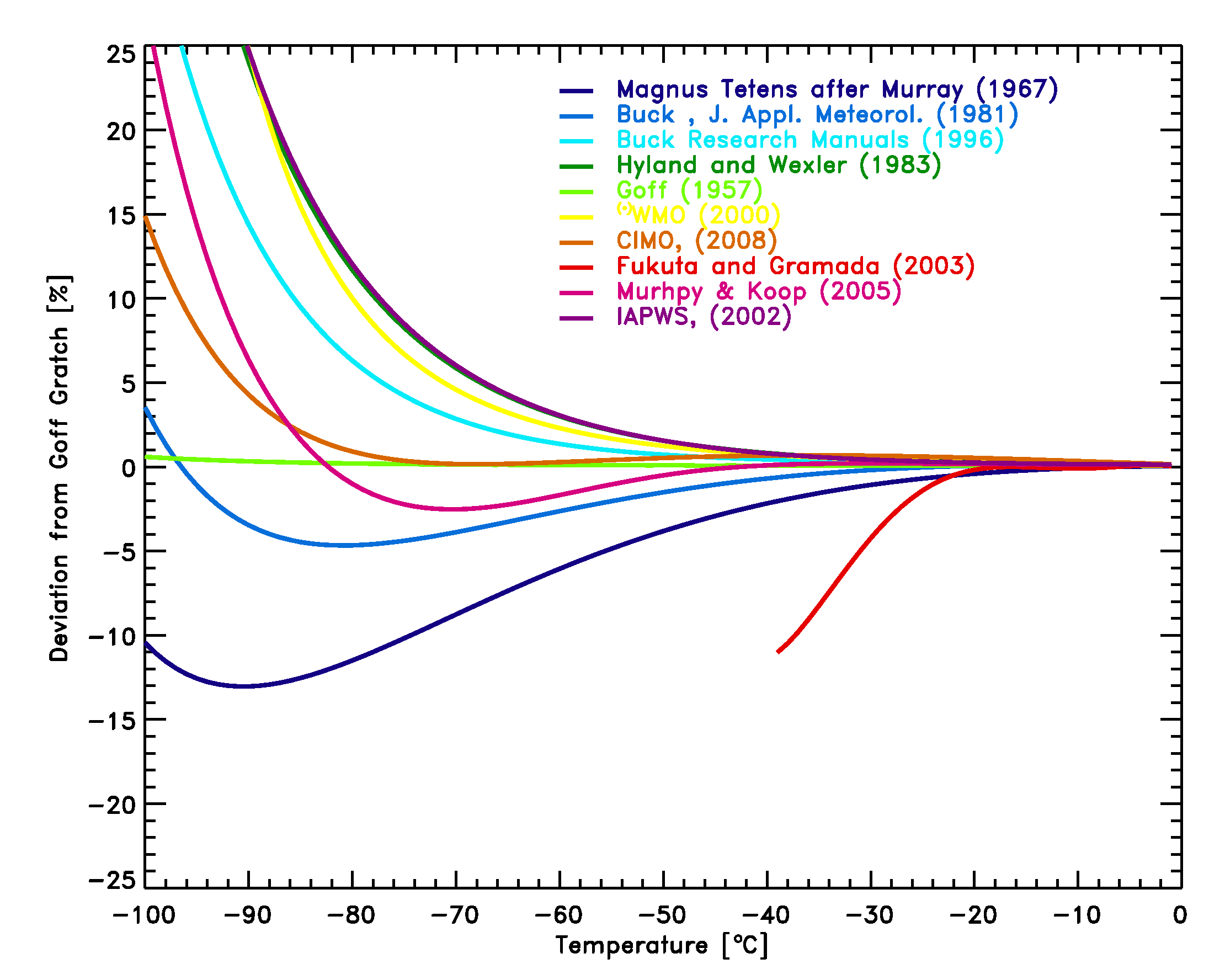
Figure 1: Comparison of equations [2]-[11] with the Goff Gratch equation [1] for the saturation pressure of water vapor over liquid water. The measurements by Fukuta et al. [2003] are shown as well.
Saturation vapor pressure formulations
Holger
Vömel
National Center for
Atmospheric Research
Earth Observing Laboratory
Boulder, CO
A large number of saturation vapor pressure equations exists to calculate the pressure of water vapor over a surface of liquid water or ice. This is a brief overview of the most important equations used. Several useful reviews of the existing vapor pressure curves are listed in the references.
| • |
Goff Gratch equation Log10 ew
= -7.90298 (373.16/T-1) |
[1] |
| • | Guide
to Meteorological Instruments and Methods of Observation (CIMO
Guide) (WMO, 2008) ew = 6.112 e(17.62 t/(243.12 + t)) with t in [°C] and ew in [hPa] |
[2] |
| • | WMO (Goff, 1957; WMO, 2012): Log10 ew
= 10.79574 (1-273.16/T) |
[3] |
| • | Hyland
and Wexler (Hyland and Wexler, 1983): Log ew
= -0.58002206 104 / T |
[4] |
| • | Hardy (Hardy, 1998): Log ew
= -
2.8365744 103 / T2 |
[5] |
| • | Buck (Buck Research Manual (1996); updated equation from Buck, A. L., New equations for computing vapor pressure and enhancement factor, J. Appl. Meteorol., 20, 1527-1532, 1981) ew = 6.1121 e(18.678 - t / 234.5) t / (257.14 + t) [1996] |
[6] |
| |
ew
= 6.1121 e17.502 t /
(240.97 + t)
[1981] with t in [°C] and ew in [hPa] |
[7] |
| • | Sonntag (Sonntag, 1994) Log ew =
-6096.9385 / T |
[8] |
| • | Magnus
Tetens (Murray, 1967) ew =
6.1078 e17.269388 * (T-273.16)
/ (T – 35.86) |
[9] |
| • | Bolton (Bolton, 1980) ew =
6.112 e17.67 * t / (t+243.5) |
[10] |
| • | Murphy
and Koop (Murphy and Koop, 2005) Log ew =
54.842763 with T in [K] and ew in [Pa] |
[11] |
| • | International
Association for the Properties of Water and Steam (IAPWS)
Formulation 1995 (Wagner and Pruß, 2002) Log (ew/22.064e6)
= 647.096/T * ((-7.85951783 ν with T in [K] and ew in [Pa] and ν = 1 - T/647.096 |
[12] |

Figure 1: Comparison of equations [2]-[11] with the Goff Gratch equation
[1] for the saturation pressure of water vapor over liquid water. The
measurements by Fukuta et al. [2003] are shown as well.
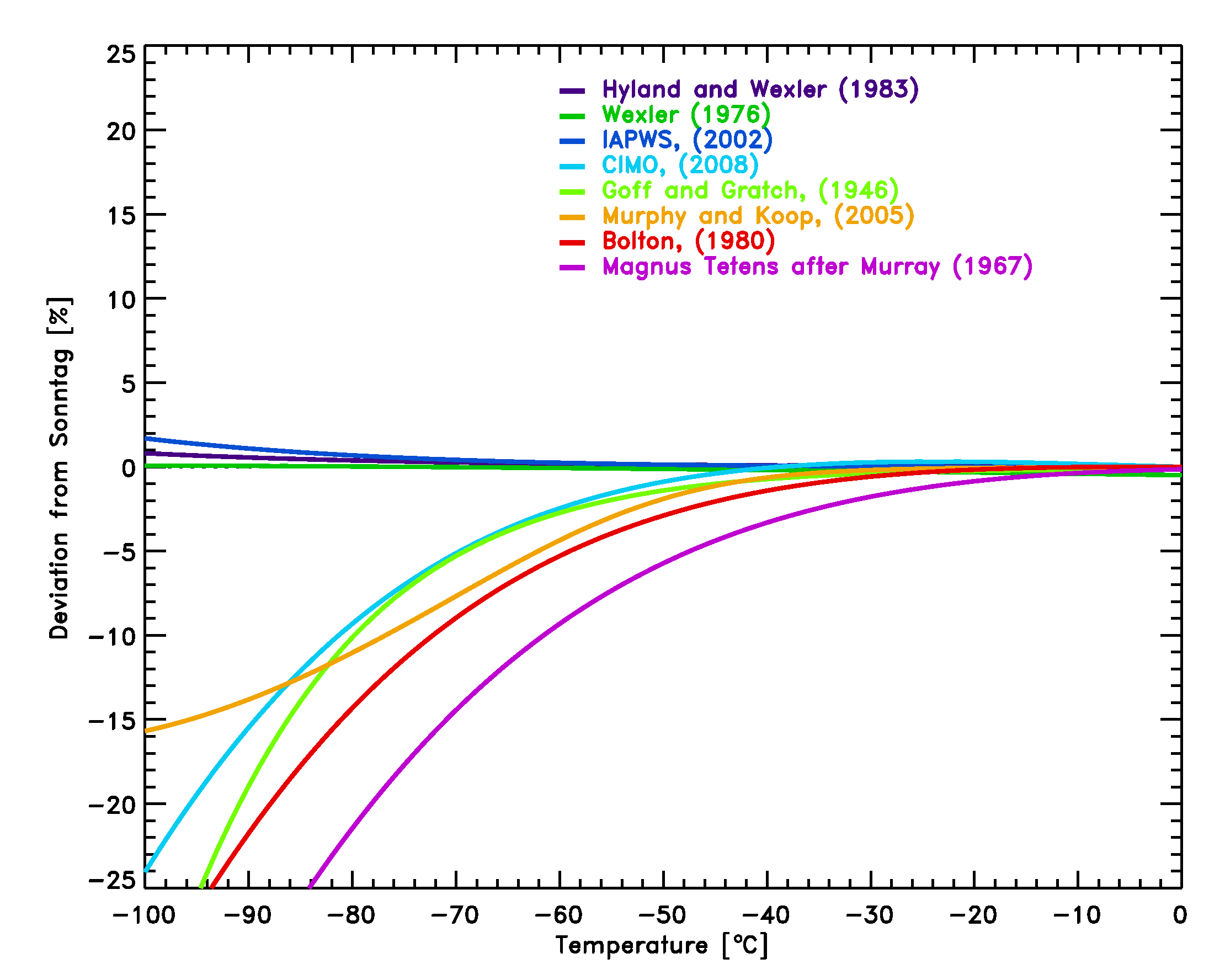
Figure 2: Comparison of several equations
with the equation by Sonntag [7] for the saturation pressure of water
vapor over liquid water.
The equations by Hyland and Wexler [4], the nearly identical equation by
Wexler (1976, see reference below) and the equation by Sonntag [7] are
the most commonly used equations among radiosonde manufacturers and
should be used in upper air applications to avoid inconsistencies.
| • |
Goff Gratch equation Log10 ei
= -9.09718 (273.16/T - 1) |
[13] |
| • | Hyland
and Wexler (Hyland and Wexler, 1983.): Log ei =
-0.56745359 104 / T |
[14] |
| • | Guide
to Meteorological Instruments and Methods of Observation (CIMO
Guide) (WMO, 2008) ei =
6.112 e(22.46 t/(272.62 + t)) |
[15] |
| • | Magnus Teten (Murray, 1967) ei =
6.1078 e21.8745584 * (T-273.16)
/ (T – 7.66) |
[16] |
| • | Buck (Buck Research Manual (1996 ei = 6.1115 e(23.036 - t / 333.7) t / (279.82 + t) [1996] |
[17] |
| |
ei
= 6.1115 e22.452 t / (272.55+t)
[1981]
with t in [°C] and ei in [hPa] |
[18] |
| • | Marti Mauersberger (Marti and Mauersberger, 1993) Log10 ei = -2663.5 / T + 12.537 |
[19] |
| • | Murphy
and Koop (Murphy and Koop, 2005) Log ei = 9.550426 |
[20] |
| • | Sonntag (Sonntag, 1994) Log ei =
-6024.5282 / T |
[21] |
Notes:
The Goff Gratch equation [13] for the
vapor pressure over ice covers a region of -100°C to 0°C. It is
generally considered the reference equation; however, other equations
have also been widely used. The equations discussed here are mostly of
interest for frost-point measurements using chilled mirror hygrometers,
since these instruments directly measure the temperature at which a
frost layer and the overlying vapor are in equilibrium. In
meteorological practice, relative humidity is given over liquid water
(see section 1) and care needs to be taken to consider this difference.
Buck Research, which manufactures
frost-point hygrometers, uses the Buck formulations in their
instruments. These formulations include an enhancement factor, which
corrects for the differences between pure vapor and moist air. This
enhancement factor is a weak function of temperature and pressure and
corrects about 0.5% at sea level. For the current discussion it has been
omitted.
The Marti Mauersberger equation is the
only equation based on direct measurements of the vapor pressure down to
temperatures of 170 K.
The comparison of equations 14-20 with the Goff Gratch equation (Figure
3) shows, that with the exception of the Magnus Teten formula, the
deviations in the typical meteorological range of -100°C to 0°C are less
than 2.5%, and smaller than typical instrumental errors of frost-point
hygrometers of 5-10%.
Not shown is the WMO recommended equation for vapor pressure over ice, since it is nearly identical with the Goff-Gratch equation [13].The equation by Sonntag (1994) agrees with Goff Gratch to within 0.19% over the typical meteorological range of -100°C to 0°C and is not shown.
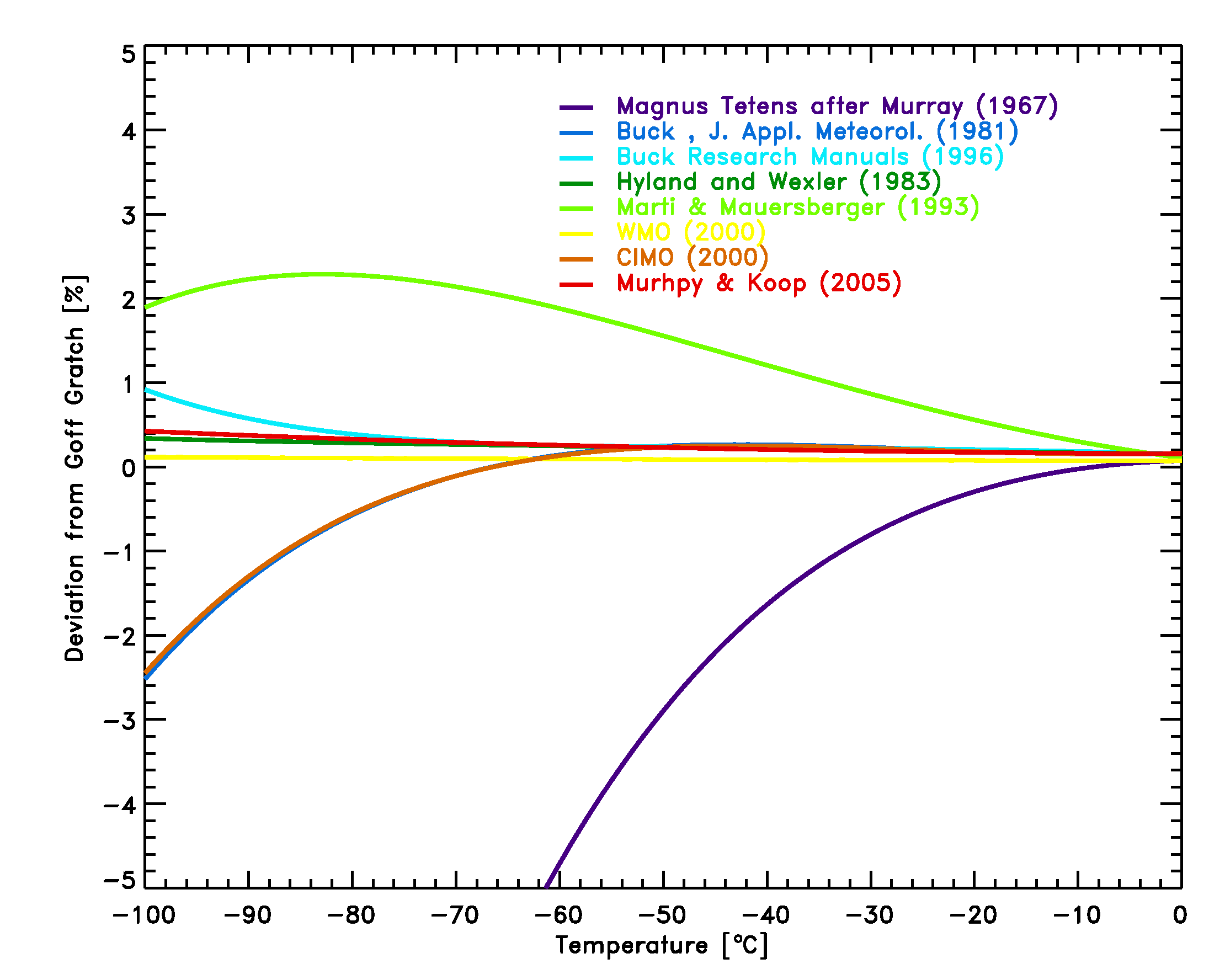
Figure 3: Comparison of equations [14]-[19] with the Goff Gratch
equation [13] for the saturation pressure of water vapor over ice.
Bolton, D., The
computation of equivalent potential temperature, Monthly Weather
Review, 108, 1046-1053, 1980..
Buck, A. L., New equations for computing vapor pressure
and enhancement factor, J. Appl. Meteorol., 20, 1527-1532, 1981.
Buck Research Manuals, 1996
Detwiler, A., Extrapolation of the Goff-Gratch formula
for vapor pressure over liquid water at temperatures below 0°C, J.
Appl. Meteorol., 22, 503, 1983.
Elliott, W. P. and D. J. Gaffen, On the utility of
radiosonde humidity archives for climate studies, Bull. Am. Meteorol.
Soc., 72, 1507-1520, 1991.
Elliott, W. P. and D. J. Gaffen, Effects of conversion
algorithms on reported upper air dewpoint depressions, Bull. Am.
Meteorol. Soc., 74, 1323-1325, 1993.
Fukuta, N. and C. M. Gramada, Vapor pressure measurement
of supercooled water, J. Atmos. Sci., 60, 1871-1875, 2003.
Gibbins, C. J., A survey and comparison of relationships
for the determination of the saturation vapour pressure over plane
surfaces of pure water and of pure ice, Annales Geophys., 8, 859-886,
1990.
Goff, J. A., and S. Gratch, Low-pressure properties of
water from -160 to 212 F, in Transactions of the American society of
heating and ventilating engineers, pp 95-122, presented at the 52nd
annual meeting of the American society of heating and ventilating
engineers, New York, 1946.
Goff, J. A. Saturation pressure of water on the new
Kelvin temperature scale, Transactions of the American society of
heating and ventilating engineers, pp 347-354, presented at the
semi-annual meeting of the American society of heating and ventilating
engineers, Murray Bay, Que. Canada, 1957.
Hardy, B., 1998, ITS-90 Formulations for Vapor Pressure, Frostpoint
Temperature, Dewpoint Temperature, and Enhancement Factors in the
Range –100 to +100 °C, The Proceedings of the Third International
Symposium on Humidity & Moisture, London, England
Hyland, R. W. and A. Wexler, Formulations for the Thermodynamic
Properties of the saturated Phases of H2O from 173.15K to 473.15K,
ASHRAE Trans, 89(2A), 500-519, 1983.
Marti, J. and K Mauersberger, A survey and new
measurements of ice vapor pressure at temperatures between 170 and 250
K, GRL 20, 363-366, 1993
Murphy, D. M. and T. Koop, Review of the vapour pressures
of ice and supercooled water for atmospheric applications, Quart. J.
Royal Met. Soc, 131, 1539-1565, 2005.
Murray, F. W., On the computation of saturation vapor
pressure, J. Appl. Meteorol., 6, 203-204, 1967.
Smithsonian Met. Tables, 5th ed., pp. 350, 1984.
Sonntag, D., Advancements in the field of hygrometry,
Meteorol. Z., N. F., 3, 51-66, 1994.
Wagner W. and A. Pruß, The IAPWS formulation 1995 for the
thermodynamic properties of ordinary water substance for general and
scientific use, J. Phys. Chem. Ref. Data, 31, 387-535, 2002.
Wexler, A., Vapor Pressure Formulation for Water in Range
0 to 100°C. A Revision, Journal of Research of the National Bureau of
Standards, 80A, 775-785, 1976.
World Meteorological Organization, Technical Regulations,
Basic Documents No. 2, Volume I - General meteorological standards and
recommended practices, Appendix A, WMO-No. 49, Geneva 2011, updated
2012.
World Meteorological Organization, Guide to
Meteorological Instruments and Methods of Observation, Appendix 4B,
WMO-No. 8 (CIMO Guide), Geneva 2008.
7 Dec. 2016
Voemel@ucar.edu